Monge array of m*n
An m-by-n matrix is said to be a Monge array if, for all 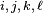 such that
such that
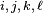 such that
such thatone obtains
So whenever we pick two rows and two columns of a Monge array (a 2 × 2 sub-matrix) and consider the four elements at the intersection points, the sum of the upper-left and lower right elements (across the main diagonal) is less than or equal to the sum of the lower-left and upper-right elements (across the antidiagonal).
This matrix is a Monge array:
For example, take the intersection of rows 2 and 4 with columns 1 and 5. The four elements are:
- 17 + 7 = 24
- 23 + 11 = 34
The sum of the upper-left and lower right elements is less than or equal to the sum of the lower-left and upper-right elements.
Suggest an algorithm such that given an array of (m*n) ,it can give output whether it is Monge or not.
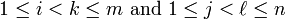
![A[i,j] + A[k,\ell] \le A[i,\ell] + A[k,j].\,](http://upload.wikimedia.org/math/a/c/e/acee0a505fa26f17301a46da794a1615.png)


What is a use of Monge array?
ReplyDelete